How to cut a rectangle into 8 squares

class. Mathematics. Nikolsky. Textbook. Answers to pg. 132

The snail, having climbed up and reached 8 m, would not go down. 1) 4 2 = 2 (m) the distance from the ground where the snail would reach on Day 1 2) 2 4 2 = 4 (m) the distance from the ground where the snail would reach on Day 2 3) 4 4 = 8 (m) the distance from the ground where the snail would reach on Day 3.

Cut a 4 × 9 rectangle into two pieces so that it can be made into a square.

Unit size cage. 4 9 = 36 squares the area of the rectangle, 36 = 6 6 so the side of the square must be equal to 6 squares.

Cut a 1 × 6 rectangle from a 10 × 7 rectangle Cut the resulting figure into two pieces so that it can be made into a square.

10 7. 1 6 = 64 squares the area of the figure, 64 = 8 8 means the side of the square must be equal to 8 squares.

The checkered paper gives an idea of how you can lay out a plane with equal squares. Figure 130 shows the ways in which tiles are laid on the floor or on the walls. The plane can also be laid out in equal rectangles. Figure 131 shows two ways to cover the floor with parquet made of equal rectangles. Come up with two more of your own parquet flooring from equal rectangles.

Task 9 T/R 76 A. Larina

A checkered square of size 6×6 is given.

a) Can this square be dissected into ten different cellular polygons in pairs?? b) Is it possible to cut this square into eleven pairwise different checkered polygons? c) What is the greatest number of pairwise different checkered rectangles we can dissect this square into?

Different unicellular polygons. 1.

Different two-cell polygons. 1.

There are 2 different three-cell polygons.

There are 5 different four-cell polygons.

than 5 different pticellular polygons.

Even if we pave the 6×6 square with all 1,2,3,4-cell different polygons, we will have only 36-(1x11x22x35x4)=7 cells. And we have to place two more polygons in them which are different from those used earlier, which is impossible.

c) We are interested in the largest number of pairwise different checkered rectangles into which this square can be dissected. So we are interested in rectangles that occupy the smallest number of cells possible.

Let’s show that it is impossible to place 9 pairwise different checkered rectangles in a given square.

Even if we place 8 different rectangles, one 1-cell, one 2-cell, one 3-cell, two 4-cell, one 5-cell, two 6-cell rectangles, it would take us 31 cells. In the remaining 5 cells should be placed a rectangle, not previously mentioned, which is impossible.

Let’s show that it is possible to place 8 paired different checkered rectangles in a given square. For example, like this:

Answer: a) yes; b) no; c) 8.

• GDZ answers in math 3 class 2 part of the textbook Dorofeev, Mirakova, Buka (Perspective)
• Page. 4
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 36
• 37
• 38
• 39
• 40
• 41
• 42
• 43
• 44
• 45
• 46
• 47
• 48
• 49
• 50
• 51
• 52
• 53
• 54
• 55
• 56
• 57
• 58
• 59
• 60
• 61
• 62
• 63
• 64
• 65
• 66
• 67
• 68
• 69
• 70
• 71
• 72
• 73
• 74
• 75
• 76
• 77
• 78
• 79
• 80
• 81
• 82
• 83
• 84
• 85
• 86
• 87
• 88
• 89
• 90
• 91
• 92
• 93
• 94
• 95
• 96
• 97
• 98
• 99
• 100
• 101
• 102
• 103
• 104
• 105
• 106
• 107
• 108
• 109
• 110
• 111
• 112
• 113
• 114
• 115
• 116
• 117
• 118
• 119
• 120
• 121
• 122
• 123
• 124
• 125
• 126
• 127

Page 11

There are lindens, birches, and maples in the park. There are 5 lindens, 7 times as many maples as lindens, and 10 more birches than maples. 1) How many maples grow in the park?? 2) How many lindens, birches, and maples are there in total?? 3) How many more maples than birches? 4) How many times fewer linden trees than birch trees? What other questions can be put to this condition?

5 д.Л_.К_|_._._._._._. 10 д.Б_|_.

1) 5 7 = 35 (д.). maples grow in the park Answer: 35 maples.2) 35 10 = 45 (д.). birches grow in the park Answer: 45 birches.3) 5 35 45 = 40 45 = 85 (д.). grows in the park Answer: 85 total trees.4) 45. 35 = by 10 (e.). more birches than maples Answer: 10 more birches5) 45 : 5 = 9 (times). less lindens than birches Answer: 9 times.

Additional questions:1) How many more maples than lindens?Solution:35. 5 = by 30 (e.). there are more maples than lindens.Answer: 30 more maples

2) How many times more maples than lindens?Solution:35 : 5 = 7 (times) more maples than lindens.Answer: 7 times.

Find the perimeter of the polygon shown in the drawing.

14 8 6 6 8 8 (14. (8. 6)) (8. (8. 6)) = 14 8 3 6 2 (14. 2) (8. 2) = 14 24 12 12 6 = 20 24 24 = 20 48 = 68 (m). perimeter of the polygon.Answer: 68 meters

4 dm 2 1 m 8 dm 1 10 dm 8 dm 10 dm

48 cm : 6 7 dm 8 cm 7 10 cm 8 cm 70 cm

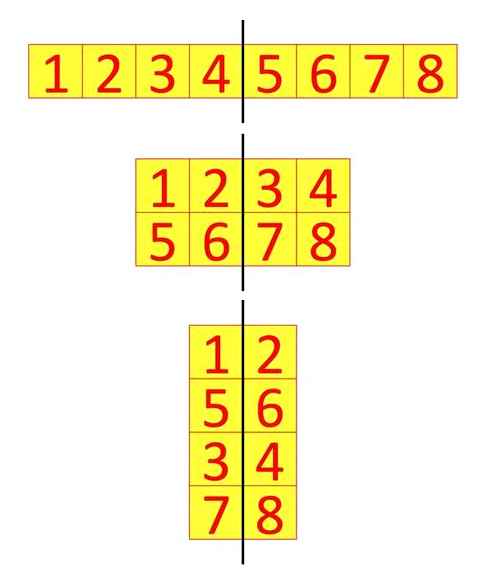
Draw a rectangle like this in your notebook and guess how to cut it into 8 squares. Draw the slash line of the cut.

Explain the rebus: YES : A = A.Try to find two solutions. The same letters correspond to the same digits.

YES : A = A, so:A A = DATHY two one-digit numbers can be multiplied by itself to produce a two-digit number, the last digit of which is equal to a one-digit number.These are numbers 5 and 6, then:

Solution 1:5 5 = 2525 : 5 = 5 Answer: 25 : 5 = 5.

Solution 2:6 6 = 3636 : 6 = 6 Answer: 36 : 6 = 6.

• You are here:
• grade 3 /
• Math /
• GDZ answers in math 3 class 2 part of the textbook Dorofeev, Mirakova, Buka (Perspective)

How to cut a rectangle into 8 squares

Prove that a 10×10 checkerboard cannot be cut along grid lines into 1×4 rectangles. (Solutions by D.Ю. Smith.)

Solution 1 Let’s divide the board into 2×2 squares and color them in a staggered order (Fig.1). Note that any 1×4 rectangle contains an equal number (2 each) of black and white cells, but with this coloring, the board has 52 black cells and 48 white cells, t.е. not equally. So it is impossible to cut a 10×10 board into 1×4 rectangles.

Solution 2 Let’s color the board diagonally in 4 colors (Fig.2). Note that any rectangle contains one cell of each of the four colors, but in this coloring on the board on 25 cells of the 1st and 3rd colors, 26 cells. 2nd and 24 cells. 4th, t.е. not equally. So the 10×10 board cannot be cut into 1×4 rectangles.

The bottom right and left corner cells were cut out of the chessboard. Can the resulting figure be cut into 1×2 dominoes?? And if you cut out the bottom right and the top left?

Can a 6×6 board be cut into dominoes so that among them there are exactly 11 horizontal? (Horizontal coloring in two colors.)

Color the drawing in four colors so that the neighboring parts are painted in different colors. Can we do with three colors?? (See the above example. Activity 6: Coloring a Geographic Map. grade 5-6).

In a 4×4 square the left cells are painted black and the rest are painted white. In one operation, you are allowed to recolor all the cells inside any rectangle with the opposite color. In three operations, how do you get a chess coloring from the original coloring?

Several grasshoppers sit on one straight line, and the distance between neighbors. are the same. Every minute, one of them jumps to a point symmetric to it relative to the other Juke. After some time, can Grasshopper Sasha be in the place where his neighbor Lyosha was sitting at the beginning??

a) Is it possible to cut the chessboard into pieces consisting of 4 squares in the shape of a “T”?

b) Is it possible to cut a 10×10 chessboard into such pieces??

Is it possible to cut an 8×8 square with the corner cut off into 1×3 rectangles??

Is it possible to cut a 10×10 board into four-cell pieces in the shape of the letter “G”?? (Horizontal coloring in two colors.)

An 8×8 board cut into 2×1 dominoes. Can there be 15 vertical and 17 horizontal dominoes?

A triangle is dissected into triangles (25 pieces), as shown in the figure. Juke can walk around the triangle, moving between adjacent (side by side) triangles. What is the maximum number of triangles a Juke can go through if it has been in each of them no more than once??

What is the largest number of rhombuses, each made of two equilateral triangles with side 1, that can be cut out of an equilateral triangle with side 5 (see. Figure. of the previous problem).

A triangular castle is divided into 100 identical triangular halls. A door is made in the middle of each wall. How many rooms can a person who does not want to visit more than once visit??

How to cut a rectangle into 8 squares

Problem 1: Can a square 5 × 5 cut into rectangles 1 × 2 (dominoes).

Problem 2: From chessboard 8 × 8 the opposite corner cells are cut out. Can the remainder be cut into rectangles 1 × 2 (dominoes)?

Solution: No. Each domino occupies one black and one white square, and the number of black and white squares on the board without corners is different.

Problem 3: From the opposite corners of the board 10 × 10 cut two squares 3 × 3. Can the remainder be dissected into dominoes??

Problem 4: Think of a connected piece on a chessboard that has an equal number of black and white squares, but cannot be broken into dominoes.

Problem 5: Is it possible to cut a square 10 × 10 into 25 figures ?

Problem 6: Is it possible to cut a square 10 × 10 into 25 pieces ?

Solutions: Color the board in staggered order. There will be an even number of black squares and each piece will have one or three.

Problem 7: Is it possible to cut the square 10 × 10 by 25 pieces ?

Color the board in four colors (see ). figure). Each figure occupies one cell of each color, and the number of cells of the first and second colors is different.

Problem 8: Is it possible to dissect a square 10 × 10 by 25 pieces ?

Solution: Paint the verticals in one.

Problem 9: Prove that a board of 8 × 8 without a corner cell cannot be dissected into rectangles 1 × 3.

Problem 10: Can a board of 8 × 8 cut into one square 2 × 2 and 15 figures of the form ?

Problem 11: Square a)5 × 5b)8 × 8 divided into several rectangles 3 × 1 and one square 1 × 1. Where can stand the square of 1 × 1?

Solution: a) In the center, b) On the third square diagonally from any corner.

Problem 12: What is the maximum number of bars 1 × 1 × 4 can be cut from the cube 6 × 6 × 6?

Problem 13: A rectangle is divided into figures and. One is lost, but replaced by. Prove that a new set cannot cover the original rectangle.

Problem 14: Is it possible to square 16 × 16 split into 64 rectangles 1 × 4, of which 31 will stand vertically, and the remaining 33 horizontally?

Solution: Paint every fourth vertical.

Problem 15: For which n squares n × n can be dissected by a) ;

Solution: For n divisible by four.

Problem 16: The rectangle m × k divided into rectangles 1 × n. Prove that m is divisible by n or k is divisible by n.

Problem 17: Prove that the rectangle m × n can be divided into rectangles a × b, if and only if the following conditions are satisfied:

1) m and n are represented as ka lb (k and l are non-negative integers)

Problem 18: Rectangle m × n is called robust if it can be broken into dominoes such that any cut of the rectangle intersects at least one domino. Prove that:

(e) If a rectangle m × n strong, then also a rectangle m × (n 2) sturdy.

(g) Which rectangles are solid and which are not?

Solution: f) Hint: every line in square 6 × 6 intersects an even number of dominoes.

g) All rectangles m × n where mn is even, m,n 5 except 6 × 6.

a) Is it possible for a rectangle 5 × 9 divide into corners?

b) Prove that a rectangle with sides greater than 100 and area divisible by 3 can be dissected into dominoes.

(c) Which rectangles can be broken into corners and which cannot?

Can a board of 2 n × 2 n without a corner cell divide into corners?

Solution: Yes, they can. Partitioning is constructed by induction.

Problem 21: At which n is the board (2n 1) × (2n 1) without a corner cell can be divided into dominoes, among which there are an equal number of vertical and horizontal?

How to cut a rectangle into 8 squares

2018-12-01 1 2. ? ( ).

1). , 2 1, 2 3 2, 2,. ,. 2) 1 frac12 (. ) 3) 4. x, 1. x, 2 x. “” 1. 2x,. 4. 8x x = frac14. 4). 6 2 “” (. ). 2(1. 2x) 2 frac1. 2x 2= 3(1. 2x),. x = frac16

Answers to page 100 71-380 GDZ for the textbook Mathematics 5 grade Merzlyak, Polonsky, Yakir

Rectangle ABCD is dissected into squares as shown in Figure 139. The side of the smallest of the squares is 4 cm. Find the lengths of the sides of rectangle ABCD.

The side of the smallest square is 4 cm, 4 3 = 12 (cm). side of the largest squareAD = BC = 12 12 4 = 28 (cm) Sides AD and BC consist of 4 middle squares28 : 4 = 7 (cm). Side of the middle squareCD = AB = 7 4 3 = 19 (cm)Answer: 28 cm and 19 cm.

Assignment 72

Draw a rectangle whose adjacent sides are 3 cm and 6 cm. Divide it into three equal rectangles. Calculate the perimeter of each of the obtained rectangles. How many solutions have the problem.

The problem has 2 solutions: 1) AK = KM = MD = BN = NP = PC = 6 : 3 = 2 (cm) P ABNK = P KNPM = P MPCD = 2 2 2 3 = 10 (cm)

2) AK = KM = MD = BN = NP = PC = 3 : 3 = 1 (cm) P ABNK = P KNPM = P MPCD = 2 1 2 6 = 14 (cm)

Problem 73

Is there any rectangle with a perimeter of 12 cm that can be dissected into two equal squares?? If the answer is Yes, draw the diagram and calculate the perimeter of each of the squares obtained.

Rectangle ABCD with sides 4 cm and 2 cm. P ABCD = 2 2 2 4 = 4 8 = 12 (cm) By dividing the rectangle in half we obtain a square with a side of 2 cm, the perimeter of which is equal: P ABEF = P FECD = 2 4 = 8 (cm) Answer: 8 cm. the perimeter of each of the squares.

Task 74

How do I divide a square into four equal parts so that two squares can be made of these parts??

Then we add a square from each pair of triangles.

Problem 75

How do you cut an isosceles right triangle into four equal pieces to make a square??

Problem 76

How to cut a rectangle with sides of 8 cm and 4 cm into four parts so that it can be made into a square?

Problem 77

How to cut a square into a triangle and a quadrilateral to make a triangle?

Put a triangle on top of a quadrilateral and you get a large triangle.

Problem 78

How to cut a square with a side of 6 cm into two pieces along a polyline of three links so that the pieces are made into a rectangle?

Problem 79

Construct line MK, ray PS, and segment AB, such that it intersects segment AB and line MK, and line MK does not intersect segment AB.

Problem 80

Lemons, oranges, and tangerines are available in the store, for a total of 740 kg. If we sold 55 kg of lemons, 36 kg of oranges, and 34 kg of tangerines, the remaining masses of lemons, oranges, and tangerines would be equal. How many kilograms of each kind of fruit are in the store?

It is not possible to divide by two because there is a misprint in the problem. In principle, you can solve this problem using fractions:

1) 55 36 34 = 125 (kg). all the fruit would have been sold 2) 740. 126 = 615 (kg). of fruit left in the store 3) 615 : 3 = 205 (kg). the mass of each of the remaining fruits 4) 205 55 = 260 (kg). of lemons available in the store 5) 205 36 = 241 (kg). there are oranges in the store 6) 205 34 = 239 (kg). answer: 260 kg of lemons, 241 kg of oranges, 239 kg of tangerines.

Presentation on Mathematics “Cutting Tasks” (Grade 5)

We pay your attention, that according to the Federal law N 273-FZ “About education in the Russian Federation” in the organizations realizing educational activity, training and education of students with physical disability both together with other students and in separate classes or groups is organized.

“The relevance of establishing school reconciliation/mediation services in educational organizations”

Certificate and tuition discount for each participant

Description of the presentation by individual slide:

“Geometry is the most powerful means of refining our mental faculties and enabling us to think and reason properly” Galileo Galilei Cutting problems

I. Historical Background The first treatise to deal with problems of dissection. Famous experts in this section of geometry were the famous classics of amusing geometry and puzzle compilers Henry E. Dewdeny and Harry Lindgren.

II. Checkered Paper Problem A square has 16 cells. Divide the square into two equal parts so that the cutting line runs along the sides of the cells. (We will consider different ways of cutting a square in two parts if the parts of the square obtained by one way of cutting are not equal to the parts obtained by another way.) How many total solutions does the problem have? Solution:

Task A 3 x 5 rectangle contains 15 squares and the center square is removed. Find five ways to cut the rest of the figure into two equal parts so that the cutting line runs along the sides of the cells. Solution:

Problem Divide a 4 x 4 square into four equal parts so that the cutting line runs along the sides of the cells. How many different ways to cut? Solution:

Task Divide the figure into three equal parts so that the cut line runs along the sides of the squares. Solution:

Task Divide the figure into four equal parts so that the mowing lines of the cuts run along the sides of the squares. Find as many solutions as possible. Solution:

Task Cut the figure, into two equal parts along the grid lines, with a circle in each part. Solution:

Task Cut this square along the sides of the cells so that all the pieces are the same size and shape, and so that each contains one circle and a star. Solution:

Problem Cut a 6×6 square of checkered paper into four equal pieces so that each piece contains three shaded cells. Solution:

Problem Cut a 4 x 9 rectangle into two equal pieces along the sides of the cells so that it can be made into a square. Solution:

Problem Cut a rectangle of 10 x 7 cells into a rectangle of 1 x 6 cells. Cut the resulting figure into two pieces so that they can be made into a square. Solution:

Problem On the checkered paper, a square of 5 x 5 cells is drawn. Show how to cut it along the sides of the cells into 7 different rectangles. Solution:

Task Divide the figures into two equal parts. (You can cut not only along the lines of the cells, but also along their diagonals.) Solution:

III. Pentamino Figures: Dominoes Triminoes Tetramino Pentaminoes Make two, three, four, five squares so that any square has a common side with at least one other square. You can make only one figure from two identical squares. dominoes. You can get a domino figure from a single domino figure by attaching another square to it in different ways. You will get two dominoes.

Problem Make up all possible tetramino shapes (from the Greek. The word “tetra” is four). How many we have? (Figures obtained by rotation or symmetrical mapping from any other ones are not considered new.). Solution:

Problem Make all possible pentaminoes (from the Greek. “penta” is five). How many of these figures are? Solution:

Problem Make up pentaminoes from pentaminoes. How many solutions have the problem for each figure? Solution:

Figure 1 has the following property. If you cut it out of paper and bend it along the line a, then one part of the figure coincides with the other part. The figure is said to be symmetrical about the line a, the axis of symmetry. Figure 12 also has a symmetry axis, even two of them. the lines b and c, but figure 2 has no symmetry axis. All possible pentaminoes

Problem How many axes of symmetry do each pentamino have?? Solution:

Problem Cut the figure along the grid lines into 4 equal pieces. Solution:

The task Cut the figure along the grid lines into 4 equal parts so that each part has a shaded hexagon. Solution:

Literature Ekimova M. А., Kukin G. П. Cutting Tasks M.: MCNMO, 2002 120с.

Methods of Teaching Mathematics in Basic and Secondary Schools in the Context of the FSES EE

Mathematics: Theory and Methods of Teaching in an Educational Organization

You could, of course, just take a ruler and measure the lengths of the segments in the figure, but this method is not very good for two reasons. First, the precision of such measurements is not very high and the answer will be only an approximation. Second, if we had the picture “at an angle,” then the true lengths of the sides would be distorted, and then we would have to think about what to do with the measurements. But it is possible to find the sides of a rectangle absolutely precisely, and you only need to know the cutting scheme for this. To do this, you need to make a system of equations, taking the lengths of the sides of the squares and rectangle as the unknowns.

As already noted in the hint, this problem is not at all on geometry (as it might seem), but on linear algebra. And it is solved quite simply. We just need not be afraid to enter a lot of notations at first.

So let x и y. width and height of the large rectangle we are looking for. Let’s number the squares as shown in Figure 1, and denote the side of the square with the number i via zi. The variables already have. And from where to take the equations? Let’s look closely at figure 1: we can see that some sides of the squares are “well” adjacent to each other. For example, the white square completes the side of the red square to the side of the orange square. Another example: White and yellow are the same height as blue and magenta. These joining conditions allow us to write the equations. We obtain a system of linear equations, which we write in two ways. First, write out the equations that correspond to the vertical joints:

Volume of Open Box Made From Rectangle with Squares Cut Out

The last equation describes the adjacency of the third and eighth squares to the right side of the rectangle. But it follows from the previous equations (check it), so further we do not take it into account. Now let’s write equations for the horizontal joints (we skip the condition for the bottom side for the same reason):

Combine everything into one system, from which we need to find x и y:

To solve systems of linear equations many methods have long been invented. But in our case we can do without involving powerful theories, but simply express one variable by another and make appropriate substitutions, gradually simplifying the system. It is convenient to express the variables in z5: z2 = 1 z5, so z1 = 2 z5, so z4 = 3 z5. You can already explicitly calculate the side of the blue square: z6 = 1 z4. z5 = 4. Continuing in this vein, it is not difficult to find the sides of the other squares, and with them the sides of the rectangle: x = 32, а y = 33.